Engineering Support
Engineering Shock & Vibration Definitions
— Although a vibration isolator will provide some degree of shock isolation, and vice versa, the principles of isolation are different, and shock and vibration requirements should be analyzed separately. In practical situations, the most potentially troublesome environment, whether it be vibration or shock, generally dictates the design of the isolator. In other applications, where both are potentially troublesome, a compromise solution is possible.
Before a selection of a vibration and/or shock/isolator can be made, the engineer should have a basic understanding of the following definitions, symbols, and terms:
Vibration
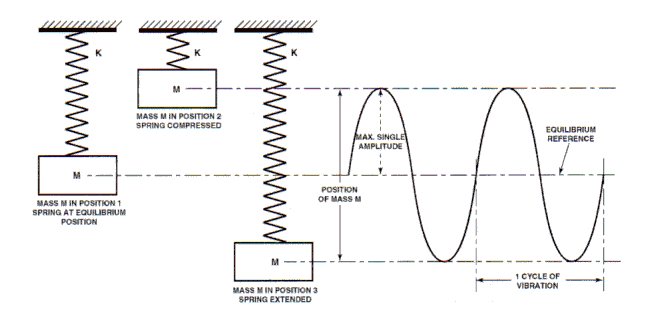
A magnitude (force,displacement, or acceleration) which oscillates about some specified reference where the magnitude of the force, displacement, or acceleration is alternately smaller and greater than the reference. Vibration is commonly expressed in terms of frequency (cycles per second or Hz) and amplitude, which is the magnitude of the force, displacement, or acceleration. The relationship of these terms is illustrated in Figure 3 below.
Frequency
Frequency may be defined as the number of complete cycles of oscillations which occur per unit of time.
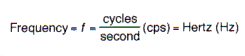
Period
The time required to complete one cycle of vibration.

Forcing Frequency
Defined as the number of oscillations per unit time of an external force or displacement applied to a system.
Forcing Frequency = fd
Natural Frequency
Natural frequency may be defined as the number of oscillations that a system will carry out in unit time if displaced from its equilibrium position and allowed to vibrate freely. (See figure 3 above).
Eq.1
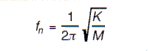
Eq. 2
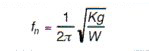
Eq. 3
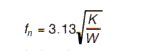
Natural frequency in terms of static deflection:
Eq. 4
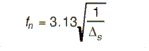
Also, natural frequency for torsional vibration:
Eq. 5

Equations 1 through 5 all neglect the effects of damping. When damping is considered, Equation 2 becomes:
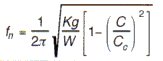
Amplitude
The amplitude of a harmonic vibration such as displacement, velocity, or acceleration is the zero to peak value corresponding to the maximum magnitude of a harmonic vibration time-history. (See Figure 3 above).
Displacement
Displacement is a vector quantity that specifies the change of the position of a body or particle and is usually measured from the mean position or equilibrium position. In general it can be represented by a translation of rotation vector or both. (See Figure 3).
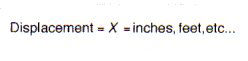
Velocity
Velocity is a vector that specifies the time rate change of displacement with respect to a frame of reference.
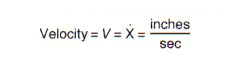
Acceleration
Acceleration is a vector that specifies the time rate of change of velocity with respect to a frame of reference. The acceleration produced by the force of gravity, which varies with the latitude and elevation of the point of observation is given by g = 980.665 cm/sec2 = 386.093 in/sec2 = 32.1739 ft/sec2, which has been chosen as a standard acceleration due to gravity.
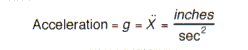
Deflection
Deflection is defined as the distance a body or spring will move when subjected to a static or dynamic force, F.
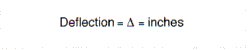
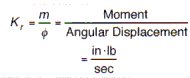
Spring Stiffness
Described as a constant which is the ratio of a force increment to a corresponding deflection increment of the spring.
Eq, 7

Rational spring stiffness:
Eq. 8
Elastic Center
The elastic center is defined as a single point at which the stiffness of an isolator or system isolators can be represented by a single stiffness value.
Damping
Damping is the phenomenon by which energy is dissipated in a vibratory system. Three types of damping generally encountered are: coulomb, hysteresis and viscous.
Coulomb Damping
If the damping force in a vibratory system is constant and independent of the position or velocity of the system, the system is said to have coulomb or dry friction damping.
Hysteresis (Inherent) Damping
Damping which results from the molecular structure of a material when that material is subjected to motion is referred to as hysteresis damping. Elastomers are good examples of materials which posses this type of damping.
Viscous Damping
If any particle in a vibrating body encounters a force which has a magnitude proportional to the magnitude of the velocity of the particle in a direction opposite to the direction of the velocity of the particle, the particle is said to be viscously damped. This is the easiest type of damping to model mathematically. All of the equations in this text are based on use of a viscous damping coefficient. Although most isolators do not use viscous damping, equivalent viscous damping usually yields excellent results when modeling systems.
Damping Coefficient
Damping for a material is expressed by its damping coefficient.
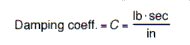
Critical Damping
A system is said to be critically damped when it is displaced from its static position and most quickly returns to this initial static position without any over-oscillation. The damping coefficient required for critical damping can be calculated using:
Eq. 9
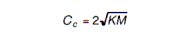
Damping Factor
The non-dimensionless ratio which defines the amount of damping in a system.
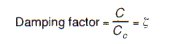
Resonance
When the forcing frequency coincides with the natural frequency of a suspension system, this condition is known as resonance.
Transmissibility
Defined as the ratio of the dynamic output to the dynamic input.
Eq. 10

For negligible damping (C/Cc=0), T becomes:
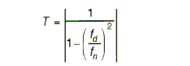
When resonance occurs, and T is at its max and Equation 10 becomes:
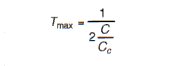
Shock
Defined as a motion in which there is a sharp, nearly sudden change in velocity. Examples of this are a hammer blow on an anvil or a package falling to the ground. Shock may be expressed mathematically as a motion in which the velocity changes very suddenly.
Shock Pulse
Shock Pulse is a primary disturbance characterized by a rise and decay of acceleration from a constant value in a very sort period of time. Shock pulses are normally displayed graphically as acceleration vs. time curves.
Shock Transmission
Shock transmitted to the object subjected to the shock. This can be calculated with the following equation:
Eq. 13
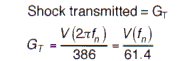
In this equation, V represents an instantaneous velocity shock. Most shock inputs can be approximated by an instantaneous velocity shock.
The associated dynamic linear deflection of an isolator under shock can be determined by the use of the following equation:
Eq. 14
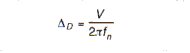
Contact Us
The personal data collected are processed, the responsibility of which is HUTCHINSON AEROSPACE & INDUSTRY INC. company, in order to respond to your request for information and/or for the purpose of commercial prospecting. Mandatory fields to be completed are marked with an asterisk. The legal basis for the processing is your consent, which you may withdraw at any time, without prejudice to previous processing operations. Personal data are reserved for the use of the HUTCHINSON group and may only be transmitted to companies of the HUTCHINSON group and/or commercial partners for commercial purposes, if you have expressly consented to this.
In accordance with the regulation relating to personal data (GDPR), you have the right of access, rectification and erasure of your personal data, as well as the right of opposition to their processing. You may request the disclosure of your personal data and you have the right to define guidelines for the treatment of your personal data after your death. You can also request the portability of your data as well as the limitation of their processing, and/or file a complaint to your local authority.
You can exercise your rights and ask us about the processing of your personal data by contacting us at the following email address: [email protected]
To find out more read our Privacy and Cookies Policy.
